PROVIDENCE, R.I. [Brown University] — Wrinkles, creases and folds are everywhere in nature, from the surface of human skin to the buckled crust of the Earth. They can also be useful structures for engineers. Wrinkles in thin films, for example, can help make durable circuit boards for flexible electronics.
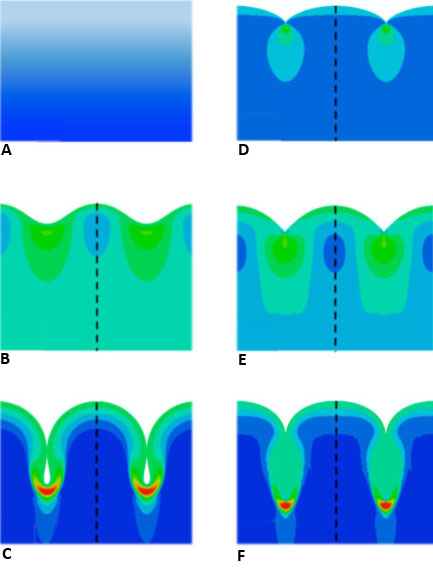
With increased compression, a flat surface with a stiffness boundary layer (a) can become a wrinkle (b) and then a fold (c). Other possibilities include an instantaneous crease (d), a wrinkle-crease (e) or a fold-crease (f).
A new mathematical model developed by researchers from Brown University could help engineers control the formation of wrinkle, crease, and fold structures in a wide variety of materials. It may also help scientists understand how these structures form in nature. The work is published in the Proceedings of the Royal Society A.
“In nature, solid materials often have stiffer surfaces and a more compliant substrate underneath. We call that stiff surface the ‘stiffness boundary layer,’” said Kyung-Suk Kim, professor of engineering at Brown, who performed the research with research associate Mazen Diab. “If you have that kind of system and you compress it, it begins to buckle and form many different patterns on the surface.”
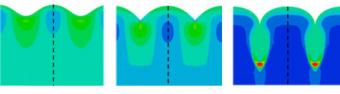
Those structures include wrinkles, creases, ridges, and folds. In a paper published last year, Kim and Diab cataloged the formation of these structures — they dubbed them “ruga” states — in a theoretical model of a rubbery solid. With this latest paper, they model the transition points between these structures as materials with a stiffness boundary layer are compressed — looking in particular at the transition from wrinkle to crease.
The model shows that at low compression, wrinkles begin to form across the surface. But as compression increases, the model identifies critical points at which groups of ripples suddenly disappear from the surface to form a single crease — a sharp depression where the stiff surface plunges down into the substrate. Knowing that point of creasing, called localization, is critically important for many applications, Kim said.
One example is in flexible electronics. Circuit elements in flexible devices are made on thin films. Those films are usually made of metal, which means they break if stretched. To prevent that, engineers place wrinkles initially into their films. Those wrinkles give the film room to stretch a bit without breaking — like a spring. But if those films are too soft and compressed too much, the wrinkles will localize into a crease. “If you get a crease into the substrate, the film will break,” Kim said. “So circuit reliability is related to this localization process.”
Kim and Diab also modeled the extent to which localization is reversible. In other words, once a crease forms in a material, how does it uncrease when compression is relaxed? They found that the compression level required to create a crease is different from what is required to undo it.
“If you have a crease and then you relax your strain a little bit, the wrinkles don’t come back right away,” Kim said. “It keeps its crease shape. We showed that you need a much more relaxed state to get the wrinkles back.”
In addition to helping engineers, Kim hopes the model that he and Diab have created will help scientists understand compression processes in natural systems as well. Human skin has a stiffness boundary like the theoretical material Kim and Diab modeled. So the model may offer insights into how wrinkles and creases form in skin and could help in designing artificial skins and soft robot grips. The human brain is covered in wrinkles and creases. Perhaps models like this, Kim says, can shed light on how compression causes brain injury.
“We are laying down the mathematical framework for understanding how this works,” Kim said.
The work was supported by the Korea Institute of Science and Technology, the Korea Institute of Machinery and Materials, and the U.S. National Science Foundation (DMR-0520651).